Understanding 10 to the Negative 4th Power: A Simple Explanation
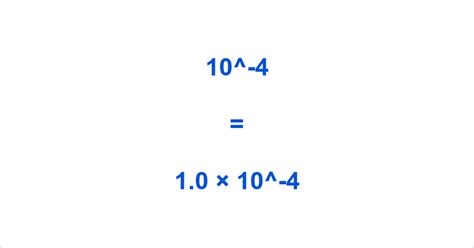
Understanding 10 to the Negative 4th Power: A Simple Explanation
Have you ever come across the term “10 to the negative 4th power” and wondered what it means? At first glance, it might seem like a complex mathematical concept, but it’s actually quite straightforward once you break it down. Let’s explore this idea step by step, using real-world examples and clear explanations to make it accessible to everyone.
What Does 10 to the Negative 4th Power Mean?
In mathematics, expressions like “10 to the negative 4th power” are written as 10^(-4). This is a form of scientific notation, which is a convenient way to represent very large or very small numbers. Here’s the breakdown:
- 10 is the base number.
- ^(-4) indicates the exponent, which tells you how many times to multiply or divide the base by itself.
When the exponent is negative, it means you’re dividing instead of multiplying. So, 10^(-4) is the same as 1 divided by 10 raised to the 4th power:
[ 10^{-4} = \frac{1}{10^4} ]
Now, calculate (10^4):
[ 10^4 = 10 \times 10 \times 10 \times 10 = 10,000 ]
Therefore:
[ 10^{-4} = \frac{1}{10,000} = 0.0001 ]
Why Use Negative Exponents?
Negative exponents are incredibly useful for expressing tiny values concisely. Instead of writing out long decimal numbers, scientists, engineers, and mathematicians use negative exponents to simplify their work. For example:
- In chemistry, the concentration of a solution might be expressed as (2 \times 10^{-5}) moles per liter.
- In physics, distances at the atomic level are often measured in units like (10^{-9}) meters (nanometers).
Real-World Applications of (10^{-4})
To better understand the scale of (10^{-4}), let’s look at some practical examples:
Medicine: A medication dosage might be prescribed as (0.0001) grams, which is equivalent to (10^{-4}) grams. This tiny amount ensures the drug is effective without causing harm.
Environmental Science: Pollution levels in water are often measured in parts per million (ppm). A concentration of (10^{-4}) ppm means there is 1 unit of pollutant for every 10,000,000 units of water.
Technology: In electronics, components like capacitors or resistors may have values expressed in microfarads ((\mu F)) or ohms ((\Omega)). A value of (0.0001) (\mu F) is the same as (10^{-4}) (\mu F).
Comparing Positive and Negative Exponents
To appreciate the difference between positive and negative exponents, let’s compare them side by side:
| Exponent | Calculation | Decimal Value |
|---|---|---|
| (10^4) | (10 \times 10 \times 10 \times 10) | 10,000 |
| (10^{-4}) | (\frac{1}{10,000}) | 0.0001 |

Historical Context: The Evolution of Exponents
The concept of exponents dates back to the 9th century, when Persian mathematician Muhammad ibn Musa al-Khwarizmi introduced the idea of powers in his algebraic works. However, negative exponents didn’t become widely used until the 17th century, when scientists like René Descartes and Isaac Newton formalized their use in mathematical notation.
Future Trends: Exponents in Modern Technology
As technology advances, the use of exponents, including negative ones, continues to grow. For instance:
- Quantum Computing: Quantum bits (qubits) operate at scales as small as (10^{-10}) meters.
- Nanotechnology: Engineers design materials with properties measured at the (10^{-9}) meter scale.
- Data Storage: Hard drives store data in bits as small as (10^{-12}) meters.
Myth vs. Reality: Common Misconceptions
Myth: Negative exponents make numbers negative.
Reality: Negative exponents indicate division, not a negative value. For example, (10^{-4}) is positive.Myth: Exponents are only used in advanced math.
Reality: Exponents are applied in everyday life, from cooking measurements to financial interest rates.
What is 10^{-4} in decimal form?
+10^{-4} is equal to 0.0001, or one ten-thousandth.
How do negative exponents differ from positive exponents?
+Positive exponents indicate repeated multiplication, resulting in large numbers, while negative exponents indicate repeated division, resulting in small fractions.
Where are negative exponents used in real life?
+Negative exponents are used in fields like medicine, environmental science, and electronics to express tiny quantities concisely.
Can 10^{-4} be written as a fraction?
+Yes, 10^{-4} can be written as \frac{1}{10,000}.
Why are negative exponents important in science?
+Negative exponents allow scientists to work with extremely small values without using cumbersome decimal notation, making calculations more efficient.
Conclusion: Mastering (10^{-4})
Understanding (10^{-4}) is more than just memorizing a number—it’s about grasping a fundamental concept that underpins science, technology, and everyday life. By recognizing that (10^{-4}) equals 0.0001, you’ve unlocked a powerful tool for working with small quantities. Whether you’re a student, a professional, or simply curious, this knowledge will serve you well in countless situations.



