Mastering Sine and Cosine Multiplication: A Simple Guide
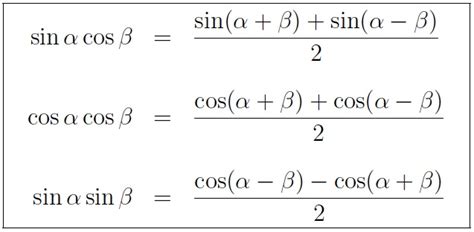
Trigonometric functions like sine and cosine are fundamental in mathematics, appearing in fields from physics to engineering. While their individual properties are well understood, multiplying them together can seem daunting at first. Fear not! This guide will break down sine and cosine multiplication into digestible chunks, providing clear explanations, practical examples, and insightful tips. Understanding the Basics
Before diving into multiplication, let’s revisit the core concepts. Sine and cosine are functions that relate the angles of a right triangle to the ratios of its sides.
Sine (sin): The ratio of the length of the side opposite an angle to the hypotenuse.
Cosine (cos): The ratio of the length of the adjacent side to the hypotenuse.
These functions oscillate between -1 and 1, reflecting the cyclical nature of angles in a circle. The Product-to-Sum Identities: Your Secret Weapon
The key to mastering sine and cosine multiplication lies in the product-to-sum identities. These identities transform products of trigonometric functions into sums or differences, simplifying calculations significantly. Here they are:
- sin(A) * cos(B) = (1⁄2) * [sin(A + B) + sin(A - B)]
- cos(A) * cos(B) = (1⁄2) * [cos(A + B) + cos(A - B)]
- sin(A) * sin(B) = (1⁄2) * [cos(A - B) - cos(A + B)]
Applying the Identities: Examples
Let’s see these identities in action with some examples: Example 1: Simplify sin(x) * cos(2x)
Using the first identity:
sin(x) * cos(2x) = (1⁄2) * [sin(x + 2x) + sin(x - 2x)] = (1⁄2) * [sin(3x) + sin(-x)]
Since sin(-x) = -sin(x), we get:
= (1⁄2) * [sin(3x) - sin(x)]
Example 2: Simplify cos(π/4) * cos(π/6)
Using the second identity:
cos(π/4) * cos(π/6) = (1⁄2) * [cos(π/4 + π/6) + cos(π/4 - π/6)] = (1⁄2) * [cos(5π/12) + cos(π/12)]
Beyond Simplification: Practical Applications
Mastering sine and cosine multiplication isn’t just about simplifying expressions. It’s a crucial skill with real-world applications:
Physics: In wave mechanics, the product of sine and cosine functions describes wave interference patterns.
Electrical Engineering: In AC circuits, the product of sine waves represents power dissipation.
Signal Processing: Fourier transforms, used in image and audio processing, heavily rely on trigonometric products.
Tips and Tricks for Success
Memorize the Identities: These are your fundamental tools. Commit them to memory for quick access.
Visualize the Unit Circle: Understanding the cyclical nature of sine and cosine on the unit circle aids intuition.
Practice Regularly: The more you work with these identities, the more natural they’ll become.
Use Technology Wisely: Graphing calculators and software can help visualize results and verify your work.
Common Pitfalls to Avoid
Misapplying Identities: Double-check that you’re using the correct identity for the given functions.
Forgetting Signs: Pay close attention to the signs in the identities, especially when dealing with negative angles.
Overcomplicating: Sometimes, simpler methods like factoring or trigonometric substitutions might be more efficient.
What are the product-to-sum identities used for?
+Product-to-sum identities are used to simplify expressions involving the product of sine and cosine functions, transforming them into sums or differences of trigonometric functions. This simplification is crucial for solving equations, integrating functions, and analyzing waveforms.
Can I use these identities for any angles?
+Yes, the product-to-sum identities are valid for any angles A and B, measured in radians or degrees. They are fundamental trigonometric relationships that hold true universally.
Are there other methods for multiplying sine and cosine?
+While product-to-sum identities are the most common method, other techniques like using complex numbers (Euler's formula) or trigonometric substitutions can also be employed in specific contexts.
How can I remember the product-to-sum identities?
+Mnemonics, flashcards, and regular practice are effective ways to memorize these identities. Focusing on understanding the underlying patterns can also aid in recall.
By embracing the power of product-to-sum identities and cultivating a strong foundation in trigonometric principles, you’ll be well on your way to mastering sine and cosine multiplication and unlocking its vast applications.