5 Ways to Convert 1/20 to a Decimal Easily
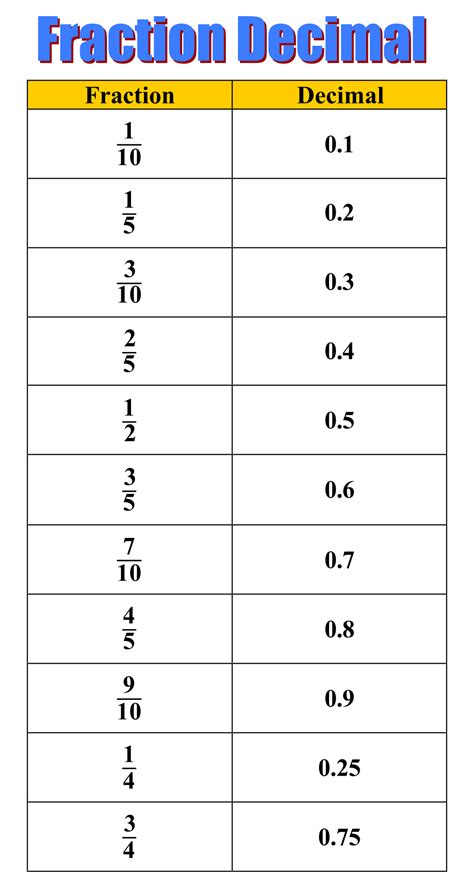
Converting fractions to decimals is a fundamental skill in mathematics, often required in various real-world applications, from finance to engineering. The fraction 1⁄20 is particularly interesting because it represents a common division that can be easily understood and applied. In this article, we’ll explore five distinct methods to convert 1⁄20 to a decimal, each with its own approach and level of complexity. Whether you’re a student, a professional, or simply curious, these methods will provide you with a comprehensive understanding of the process.
Method 1: Direct Division
The most straightforward way to convert a fraction to a decimal is by performing the division directly. For 1⁄20, this involves dividing 1 by 20.
- Set up the division: 1 \div 20
- Perform the division: 20 goes into 1 zero times, so you add a decimal point and a zero after the 1 , making it 1.0 .
- Continue dividing: 20 goes into 10 zero times, so add another zero, making it 100 .
- Final step: 20 goes into 100 five times, so the result is 0.05 .
Thus, 1⁄20 as a decimal is 0.05.
Method 2: Using Equivalent Fractions
Another approach is to convert the fraction to an equivalent form with a denominator that is a power of 10, making the conversion to a decimal more intuitive.
For 1/20, multiply both the numerator and denominator by 5 to get a denominator of 100:
\[ \frac{1 \times 5}{20 \times 5} = \frac{5}{100} \]This directly translates to 0.05 in decimal form.
Method 3: Decimal Long Division
Decimal long division is a systematic method for converting fractions to decimals, especially useful for larger denominators.
- Write the fraction as a division problem: 1.000 \div 20
- Divide step-by-step:
- 20 goes into 10 zero times, so write 0 and bring down the next 0.
- 20 goes into 100 five times, so write 5.
- Result: The quotient is 0.05.
Method 4: Using a Calculator
While not the most educational method, using a calculator is the quickest and most efficient way to convert 1⁄20 to a decimal.
Simply input 1 ÷ 20 into any calculator, and it will display 0.05 instantly. This method is ideal for verifying your manual calculations.
Method 5: Mental Math and Estimation
For those who prefer mental math, estimating the decimal equivalent of 1⁄20 can be done by breaking it down into simpler components.
- Recognize the pattern: \frac{1}{20} is half of \frac{1}{10} , which is 0.1.
- Calculate: Half of 0.1 is 0.05.
Practical Applications of 0.05
Understanding 1⁄20 as 0.05 has numerous practical applications:
- Finance: Representing a 5% discount or interest rate.
- Cooking: Measuring 5% of an ingredient in a recipe.
- Engineering: Scaling down measurements by 5%.
"Mathematics is not about numbers, equations, computations, or algorithms; it is about understanding." – William Paul Thurston
Comparative Analysis of Methods
Below is a comparison of the methods discussed:
| Method | Ease of Use | Speed | Educational Value |
|---|---|---|---|
| Direct Division | Moderate | Medium | High |
| Equivalent Fractions | Easy | Fast | High |
| Decimal Long Division | Complex | Slow | High |
| Calculator | Very Easy | Instant | Low |
| Mental Math | Easy | Fast | Medium |

What is 1/20 as a decimal?
+1/20 as a decimal is 0.05.
How do you convert a fraction to a decimal without a calculator?
+You can convert a fraction to a decimal by performing long division or finding an equivalent fraction with a denominator that is a power of 10.
Why is 1/20 equal to 0.05?
+1/20 is equal to 0.05 because dividing 1 by 20 results in 0.05, or equivalently, 5/100, which is 0.05 in decimal form.
Can 1/20 be simplified further?
+No, 1/20 is already in its simplest form since 1 and 20 have no common factors other than 1.
How is 0.05 used in real life?
+0.05 is commonly used to represent 5% in finance, discounts, interest rates, and measurements in various fields like cooking and engineering.
Conclusion
Converting 1⁄20 to a decimal is a simple yet essential skill that can be approached in multiple ways. Whether you prefer the precision of long division, the speed of a calculator, or the simplicity of mental math, each method offers unique insights into the process. By mastering these techniques, you’ll not only enhance your mathematical abilities but also gain a deeper appreciation for the versatility of fractions and decimals in everyday life.
Remember, 1⁄20 = 0.05, and this knowledge can be applied in countless practical scenarios, from calculating discounts to scaling measurements.

